Defining New Scores • adoptr

library(adoptr)

In addition to the already existing ones, adoptr allows the user to implement custom scores. Usually, this will be done by defining a new sub-class of ConditionalScore. Assume that one would be interested in the probability of early stopping for futility. First we create a new class as subclass of ConditionalScore

setClass("FutilityStopping", contains = "ConditionalScore")

# constructor
FutilityStopping <- function() new("FutilityStopping")

We only need to implement a method evaluate(), all other methods are inherited from the abstract class ConditionalScore.

setMethod("evaluate", signature("FutilityStopping", "TwoStageDesign"),
          function(s, design, x1, optimization = FALSE, ...) 
              ifelse(x1 < design@c1f, 1, 0)
)

The optimization flag here allows to compute scores differently during the optimization procedure. This is, e.g., used for the evaluation of conditional power which uses adaptive Gaussian Quadrature for maximal precision by default but non adaptive Gaussian Quadrature with the pre-defined integration rule of the design object during optimization for speed.

The score can now be integrated using the expected method for conditional scores

pr_early_futility <- expected(
  FutilityStopping(), 
  Normal(), PointMassPrior(.0, 1)
)

and the resulting integral score can be evaluated as usual. Consider again, the design

design <- TwoStageDesign(
    n1  = 100,
    c1f = .0,
    c1e = 2.0,
    n2_pivots = rep(150, 5),
    c2_pivots = sapply(1 + adoptr:::GaussLegendreRule(5)$nodes, function(x) -x + 2)
)

plot(design)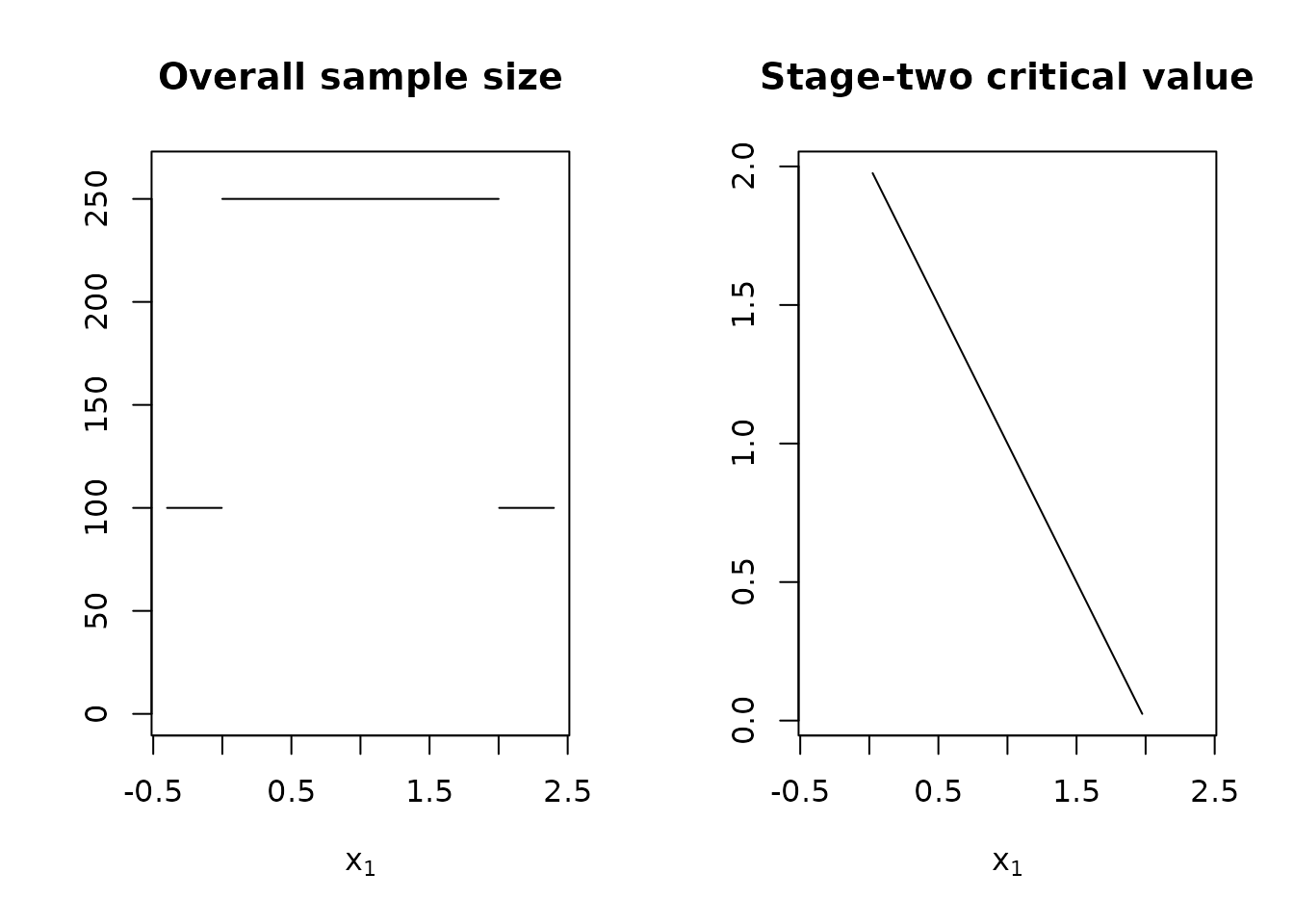

Then the value of the expected score is given by

evaluate(pr_early_futility, design)
#> [1] 0.5

The value is correct since it needs to conform with

pnorm(design@c1f)
#> [1] 0.5